
مقدمة
معرفة عدد الأبنية المستعملة في لغة ما مهمّ جداً ويمكن أن يساهم في الإجابة على تساؤلات لا تزال عالقة في نظرية تاريخ ونشأة اللغة، كتلك التي تتعلق بماهية اللغة الأم الأولى التي بدأ بها الإنسان النطقَ على هذهِ الأرض، وتلك التي تتساءل عن أيّ اللغات اليوم التي قد تكون الأقرب إلى اللغة الأم، كما تسهم هذهِ المعرفة في تعليمية اللغة فتفيد المعلّم والمتعلّم في تحصيل الزاد الكافي للإلمام بلغة ما، فكان من الوجوب أن يكون لكل المعاني التي قد يتصورّها العقل أو تخطر على المرء – من أبنية تحملها؛ في هذه المقالة نتطرق إلى جهود علماء اللغة القدامى وغيرهم في حصر عدد الأبنية والبداية تكون مع الخليل بن أحمد الفراهيدي (ت 170 هـ) مؤلّف معجم "العين" والذي تصدّره بمقدمة تعتبر الأساس الذي قام عليه فقه اللغة والانطلاقة التي ابتدأ منها خًلفه فهم عيال في بحر علمه، وسنبيّنُ الجانب الرياضي في هذه الجهود، وإضافتنا تتمثّل في محاولة حصر عدد الأبنية من خلال اعتماد نظرية "تباعد المخارج للحروف" التي تتصف بها الأبنية وفق خصائص وضعها اللغويون.
المبدأ الأساسي للعدّ
المبدأ الأساسي للعدّ هو المبدأ القائل أنّ عدد الخيارات لتحقيق تجربة مركّبة من عدد معيّن من التجارب البسيطة هو جداء عدد الخيارات الفرعية لهذه التجارب، وقد عُرِف منذ القدم فثبت استخدامه عند الصينيين في الأدب الصوفي والفلسفي لمعرفة عدد التشكيلات الممكنة من اليين واليانغ في كتاب "التباديل" وذلك حوالي 1150 قبل الميلاد، وعند اليونان لدى اكسينوقراط تلميذ افلاطون لمعالجة مسائل لسانية حوالي سنة 330 قبل الميلاد ، ووجد عند العرب في صور ومجالات شتى من المعرفة عند اللغويين كالخليل وبن دريد وفي الكيمياء عند بن حيّان وعند البيروني وبالموازاة كان مبحثا رياضيا تطرّق اليه أمثال الكرجي (ت 429 هـ) وبن منعم العبدري (ت 626 هـ) الطوسي (ت 672 هـ) وبن البنّا (ت721 هـ).
أطلق عليه بن دريد (ت 321هـ) "ضرب من الحساب واضح"، ويبدو أنّ هذا المبدأ كان مشتهرا بـ "القسمة العقلية" بعدما راجت المباحث الكلامية في الحضارة العربية ـ الإسلامية، يقول بن الأثير الكاتب (ت 637 هـ) في باب صحة التقسيم وفساده: "ولسنا نريد بذلك ههنا ما تقتضيه القسمة العقلية، كما يذهب إليه المتكلمون … ألا ترى أنّ هذه القسمة صحيحة من حيث العقل، لإستيفاء الأقسام جميعها، وإن كان من جملتها ما يستحيل وجوده" .
اللغة في عين الخليل
يرى الخليل أنّ اللغة العربية تتكوّن من 29 حرفا منها 25 حرفا صِحاحا وهي: ع ح هـ خ غ ق ك ج ش ض ص س ز ط د ت ظ ذ ث ر ل ن ف ب م، وسمّاها صِحاحا لأنّ لكل منها مَدْرجة من مدارج اللسان، بالإضافة إلى 4 أحرف ليس لها مدارج سمّاها أحرف جُوْف لأنّ ليس لها حَيّزا تُنسب إليه إلا الجَوْفَ وهي: و ا ي ء.
وصَنّفَ كلامَ العرب بحسب بنائه من هذه الحروف إلى 4 أصناف: ثُنَائِيِّ، ثلاَثِيّ، رُّباعيّ، خماسيّ؛ ويرى أنّ أيّ بناء يزيد عن خمسة أحرف في فعل أو اسم ففيه من الأحرف ما ليست أصلية فيه، وأنّ الاسم لا يكون أقلَّ من ثلاثةِ أحرف: حرف يُبْتَدَأُ به وحرف يُحشى به وحرف يُوْقَفَ عليه، ويذهب بن جنّي إلى أنّ أكثر الأبنية استعمالاً وأعدلها تركيباً الثلاثي. وهناك خاصيّة جوهرية في هذهِ الأبنية لَفَتَ اليها الخليلُ جمهورَ اللغويين الذين جاءوا من بعده حينما رتّب معجمه على قدر مخرج الحروف من الحلق وهو ترتيب سيلقي بظلاله على طبيعة الأبنية فالجواليقي يقدّر أنّ أحسن أمثلة العرب ما بني من الحروف المتباعدة المخارج، ويذهب ابن منظور الى أعمق من ذلك فيرجع تقارب الحروف من بعضها البعض وتباعدها الى سرّ في النطق يكشفه من تعنّاه.
التقليبات المحلّية
قال الخليل: اعلم أنّ الكلمة الثنائيَّةَ تَتَصَرَّف على وَجْهَيْن نحو: قَدْ، دَقْ، شَدْ، دَشُ والكلمةُ الثلاثَّيُة تتصرَّفُ على ستة أوجُه، وتُسمَّى مَسدُوسة وهي نحو: ضرب ضبر برض بضر رضب ربض، والكلمة الرباعية تتصرَّف على أربعة وعشرين وجها وذلك أن حروفها وهي أربعة أحرف تضرب في وجوه الثلاثيِّ الصَّحيح وهي سَّتة أوجه فَتصيرَ أربعة وعشرين وَجْهاً، يُكَتَب مُسْتَعْمَلها ويُلغى مُهْمَلها، وذلك نحو عبقر تقول منه: عقرب عبرق عقبر عبقر عرقب عربق قعرب قبعر قبرع قرعب قربع رعقب رعبق رقعب رقبع ربقع ربعق بعقر بعرق بقعر بقرع برعق برقع، والكلمة الخماسية تتصرّف على مائة وعشرين وجها وذلك أن حروفها وهي خمسة أحرف تُضرَب في وُجُوه الرُّباعيِّ وهي أربعة وعشرون حرفا فتصير مائة وعشرينَ وَجْها يُسْتَعْمَل أقَلُّه ويُلغى أكثره .
استطاع الخليل من خلال ايجاد "أوجه التصرّفات" لمجموعة من الحروف أو ما يمكن أن نطلق عليه "التقليبات المحلّية":
- أن يدرك استخدام مفهوم الجداء كأداة فاعلة ووظيفية تغني عن عملية الإحصاء والعد الذي يستند في أساسه للجمع. أن يكتشف العلاقة الموجودة بين عدد الأبنية التركيب الثنائي وعددها في الثلاثي والأمر نفسه بالنسبة للثلاثي والرباعي ثمّ الرباعي والخماسي.
- أن يؤسّس لمفهوم المبدأ الأساسي للعدّ.
- أن يؤسّس لمفهوم التبديلة وكنتيجة مباشرة له أن يؤسّس لمفهوم العاملي.
الجدول التالي رقم (1) يلخّص عدد التقليبات المحلّية عند الخليل:
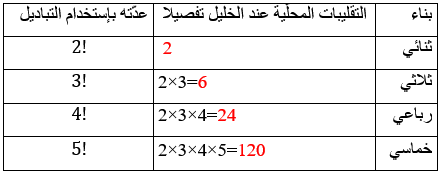
ونجد بن دريد يوضّح كيفية حساب عدّة الأبنية من الثلاثي بمثال تخطيطي وذلك بإستخدام دائرة من خلال استقراء كل التقليبات المحلّية الثلاثية الممكنة دون تكرار حرف فيقول: "ثم أَدرْ دَارَةً فوّقع ثلاثة أحرف حَواليها ثم فُكَّها من عند كل حرفٍ يمنة ويسرة حتى تُفَكّ الأحرفُ الثلاثة فيخرج من الثلاثي ستة أبنية"، ولعلّ هذا النهج قد أخذه عن الخليل.
عدد الأبنية
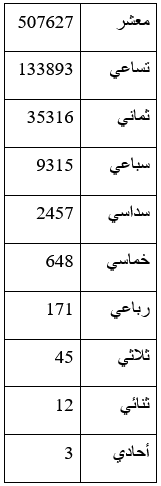
لعلّ أبرز قول يشير الى عدد الأبنية في اللغة العربية دون تكرار الحروف المهمل والمستعمل منها – يرجع الى النص التالي الذي ذكره جلال الدين السيوطي (ت 911 هـ) في كتاب المزهر: "وذكر حمزة الأصبهاني في كتاب الموازنة فيما نقله عنه المؤرخون قال ذَكَر الخليل في كتاب أن مبلغ عدد أبنية كلام العرب المُسْتَعمَل والمهمل على مراتبها الأربع من الثنائيّ والثلاثي والرباعي والخماسي من غير تكرار اثنا عشر ألف ألف وثلاثمائة ألف وخمسة آلاف وأربعمائة واثنا عشر: الثنائيّ سَبعمائة وستة وخمسون والثلاثي تسعة آلاف ألف وستمائة وخمسون والرباعي أربعمائة مائة ألف وواحد وتسعون ألفاً وأربعمائة والخماسي أحد عشر ألف ألف وسبعمائة ألف وثلاثة وتسعون ألفاً وستمائة" .
لم نجد هذا القول المنسوب للخليل بن أحمد في مقدمة كتابه العين، فإن كان قد ضاع نصه في المخطوط الأصلي أو نقل من كتاب آخر غير العين – فنحن هنا أمام فرضين في تبرير كيفية ايجاد هذا العدد.
الفرض الأول
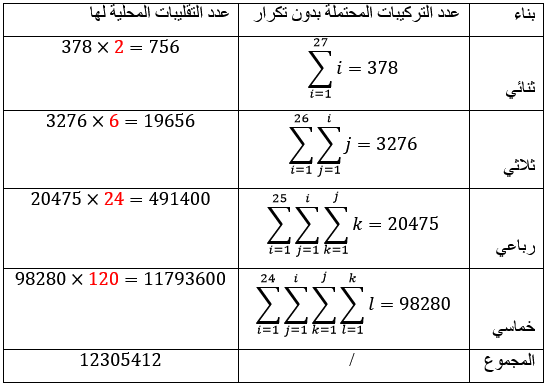
قام الخليل بربط الحروف فيما بينها بدون تكرار للحرف في البناء بإستخدام مخطط فين وبالاستقراء تبيّن له أنّ ذلك يؤول الى مجاميع متتالية حسابية، ثمّ ضرب الناتج في عدد التقليبات المحلّية، وإن كانت هذهِ هي الطريقة التي اعتمدها الخليل فنحن أمام عقلية رياضية فذّة نظرا لأنّ ذلك يتطلّب معرفة بمجموع متتالية حسابية والأهمّ من ذلك آلية الإستقراء التي استخدمها في إنشاء مجاميع مركّبة.
الجدول التالي رقم (2) يوضّح كيفيات حساب عدد الأبنية حسب الفرض الأول:
الفرض الثاني
قام الخليل بإستخدام المبدأ الأساسي للعدّ، وكانت النتائج كما يلي في الجدول رقم (3):
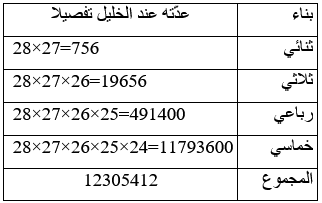
وهذا الفرض يتواءم أيضا مع قدرات الخليل والتي تجلّت أيضا في استقرائه لعروض الشعر ووضعه ميزانا لعيار الشعر، فالحسّ الرياضي كان دائما حاضرا في تقعيداته النظرية. غير أنّنا هنا يجب أن نشير الى أنّ الخليل قد اعتبر عدد حروف اللغة العربية 29، ما قد يثير تساؤلا حول ما إذا كان إحصاء عدد الأبنية قد قام به شخص آخر ذو نزعة رياضية
بن دريد على خُطَى الخليل
نجد هذا الفرض قد تبنّاه بن دريد (ت 321 هـ) أيضا وأشار الى مفهوم المبدأ الأساسي للعدّ بأنّه "ضَرْب من الحساب واضح"، وقد استخدم المبدأ الأساسي للعدّ في ايجاد عدد الأبنية الثنائية وأعطى توجيهات فيما يخصّ ايجاد عدد الأبنية الثلاثية والرباعية من خلال حساب عدد الأبنية الصحيحة والمعتلّة والممزوجة.
الجدول التالي رقم (4) يلخّص ما أورده بن دريد في حساب عدد الأبنية:
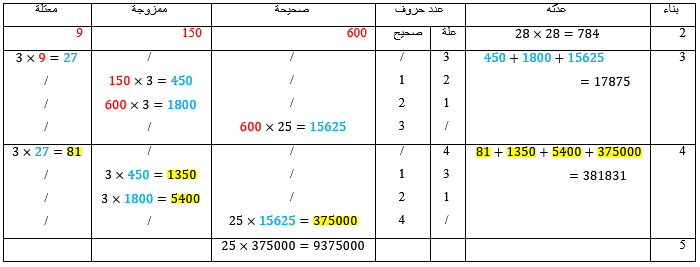
نلاحظ في السطر الأول أنّ العدد 600 ناتج عن جداء 25 حرفا صحيحا بـ 24 حرفا صحيحا، و150 ناتج عن جداء 3 حروف معتلّة بـ 25 حرفا صحيحا والحاصل في 2 عدد التقليبات، 9 هي جداء 3 حروف معتلّة بـ 3 حروف معتلّة.
اكتفى بن دريد بحساب الأبنية الأقل من خمسة أحرف. في البناء الخماسي إذا قمنا بإيجاد عدد الأبنية الصحيحة فإنّ ذلك سيفوق 9 ملايين بالإضافة الى عدد الأبنية المعتلّة والممزوجة الذي قد يصل الى بضعة عشر الف فالمجموع لا يفوق 9 ملايين ونصف. مجموع كل الأبنية حسب بن دريد لا يفوق 10 ملايين بناء.
العين من جديد
فيما يلي جدول رقم (5) يلخّص ما أورده الزبيدي (ت 379 هـ) صاحب "مختصر العين" من إحصائيات حول عدد الأبنية:
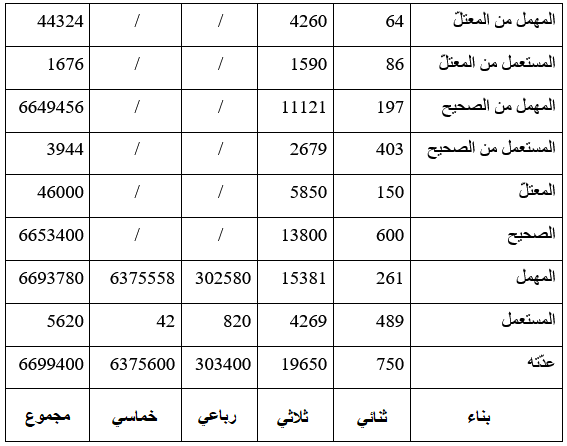
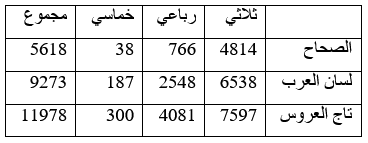
في هذا الجدول الإحصائيات لا تتوافق مع المبدأ الأساسي للعدّ، ولا نعلم إن كان الزبيدي ناقلا لها، أو تبنّى المبدأ الأساسي للعدّ وقام بإدخال تعديلات على خيارات الحسابات، وبالمحصّلة فعدد الأبنية عنده لا يتجاوز 6700000 بناء. وفيما يلي جدول رقم (6) يلخّص عدد الأبنية في كل من معجم "الصحاح" للجوهري (ت 370 هـ)، "لسان العرب" لابن منظور (ت 711 هـ)، "تاج العروس" للمرتضى الزبيدي (ت 1205 هـ) كما أوردها د. علي حلمي موسى:
بين الحركات والسكون: لغة حيّة ومواليد جدد.
يقول بن منعم العبدري (ت 626 هـ) في كتابه فقه الحساب الباب الأول النوع الحادي عشر في الكلمات التي لا يتكلم فيها البشر إلا بإحداهن: "وليكن اصطلاحنا في مثالنا هذا في عدّة حروف أبجد أن يكون ثمانية وعشرين، وأن تكون أكبر كلمة من عشرة أحرف بالزوائد والتكرير، مثل أرسطوطاليس، وأن يتعاقب على الحرف الواحد ثلاث حركات وساكن، وأن لا يبدأ بساكن، ويتوالى ساكنان" . كان بن منعم يدرك غنى اللغة العربية من خلال دور الحركة والسكون في توليد معاني جديدة في البناء ذاته فتناولها لمعرفة عدد تقلّباتها في الأبنية فكانت نتائجه بتطبيق المبدأ الأساسي للعدّ كما يلي في الجدول رقم (7):
ومن خلال تناوله للأبنية المكوّنة من حروف مكرّرة استخدم المبدأ الأساسي للعدّ في مفهوم أوسع عرف في اصطلاحنا الحديث بـ التبديلة بتكرار، ومن خلال إعطائه أمثلة يوضّح أنّ عدد الأبنية نظريا يفوق المليارات، وبهذا العمل يؤكّد بن منعم بتأليفه هذا النضج الذي بلغته الرياضيات العربية في تلك الفترة.
اللغات في ميزان واحد
بصفة عامّة عدد الألفاظ في أيّ لغة يُعطَى بالعلاقة التالية الناتجة عن مجموع متتالية هندسية:
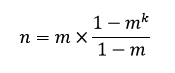
حيث: m عدد حروف هذه اللغة، k عدد الحروف الأقصى الذي يمكن أن تتشكّل منه ألفاظ هذه اللغة؛ مع أخذ k≥1.
في اللغة العربية لدينا باعتبار أنّ حرف الألف يتميّز عن ألف المد فعدد الحروف في اللغة العربية عمليا هو 29 أي m=29، وعلى اعتبار أنّ بداية البناء لا يبتدىء بألف مد وأنّ أقصى تركيبة للبناء هي خمسة أحرف أي k=5فيكون لدينا عدد الأبنية نظريا هو: 21243689 بناء حسب المبدأ الأساسي للعدّ وكما هو مبيّن في الجدول التالي رقم (8):
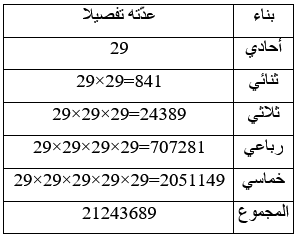
هنا نلاحظ الفرق الهائل والعدد الكبير الذي سيضاف الى اللغة العربية من خلال التمييز بين ء و ا ، أي باعتبار عدد الحروف هو 29، يقدّر هذا العدد بـ 8205736 أي ما يعادل نسبة %66.68 (اضافة ثلثين).
لغة الضاد: بين التنافر والتآلف.
فيما يلي نستعرض قاعدتين أساسيتين في تركيب الأبنية المستعملة في اللغة العربية:
يؤكّد الخليل أنّ أيّ بناء رباعي أو خماسي لا يخلو على الأقل من حرف من حروف الذلاقة والحروف الشفوية والا فهو بناء مبتدع ليس من كلام العرب، وحروف الذلاقة هي: ر ل ن، وسميت كذلك لأنّها خرجت من ذلق اللسان، والحروف الشفوية هي: ف ب م، ويعزو الخليل كثرة ورودها في الأبنية لسهولتها على اللسان في المنطق؛ وقد أثبت د. علي موسى حلمي صحّة هذهِ الخاصّية من خلال إحصاء تكرّر الحروف فوجد أنّ أكثر الحروف تكرارا في البناء الثلاثي هي: ر ن م، وفي البناء الرباعي والخماسي: ر ل ن.
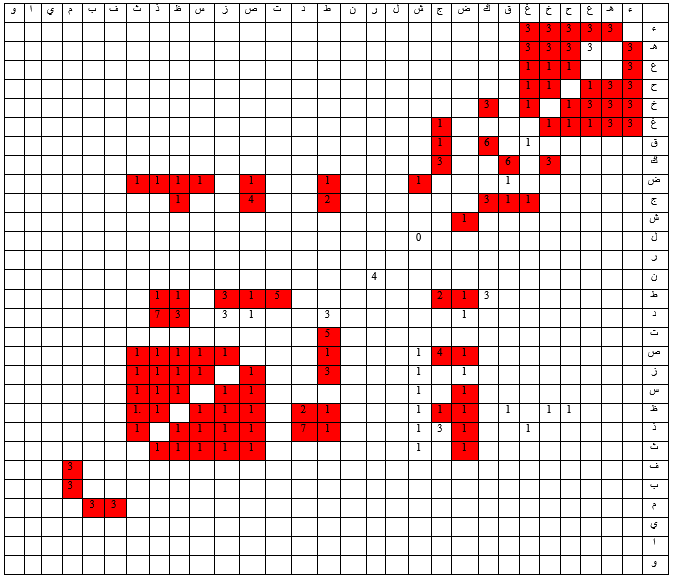
الجدول التالي رقم (9) ملخّص لأهمّ القواعد التي أقرّها اللغويون في الحروف المتنافرة ويقصد بها تلك الحروف التي لا يمكن أن تقترن مع بعضها البعض، وقد اعتمدنا ترتيب سيبويه في مخارج الحروف يقول د. أحمد بن محمد بن أحمد القرشي : "اختلف سيبويه مع الخليل في عدد مخارج الحروف، وانقسم العلماء من القرّاء والنحويين إلى مذهبين: مذهب يؤيّد الخليل وهم قلّة؛ ومذهب يؤيّد سيبويه وهم الجمهور … والراجح هو ماذهب إليه سيبويه لأنّه مذهب الجمهور من القُراء والنحويين فقد قال به: المبرد وابن السراج وابن جني والزجاجي والصيمري والزمخشري وابن الباذش وابن أبي مريم وأبو البركات ابن الأنباري والشاطبي وابن الحاجب وابن يعيش وابن عصفور وابن مالك وابن عقيل والسلسيلي والرضي وأبو حيّان الأندلسي والجاربردي، والسيوطي وغيرهم" كما اعتمدنا كتاب علم التعمية في إحصاء هذه حالات التنافر ؛ الجدول يتشكّل من 29 سطرا و29 عمودا، السطر والعمود الأولان مملوءان بالحروف مرتّبة على طريقة الخليل، الخانة الحمراء تدلّ على أنّ حرفي السطر والعمود الناتجة عن تقاطعهما هما حرفان متنافران تقديما وتأخيرا بينما الخانة المرقّمة بدون لون فتعني عدم إمكانية مجيء حرف العمود بعد حرف السطر، أمّا الأرقام فترمز إلى العلماء اللغويين الذين أشاروا إلى هذه القواعد كما يلي:
0: الخليل، 1: الكندي (ت 260 هـ)، 2: بن دنينير (ت 627 هـ)، 3: بن الدريهم (ت 762 هـ)، 4: الجواليقي، 5: بن المظفر، 6: المرتضى الزبيدي، 7: بن منظور.
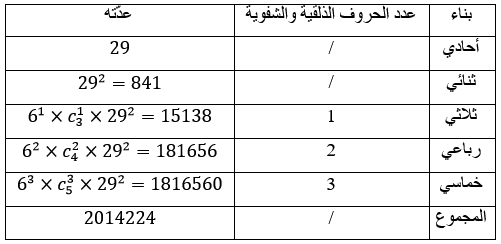
سنحسب أولا عدد الأبنية التي تحتوي على أحد حروف الذلاقة أو الحروف الشفوية بناء على القاعدة رقم وسنفترض أنّ هذه الحروف تشكّل ما يقارب ما نسبته بين 50 % و 60 % من تركيب هذه الأبنية، فتكون النتائج كما هي مبيّنة في الجدول رقم (10):
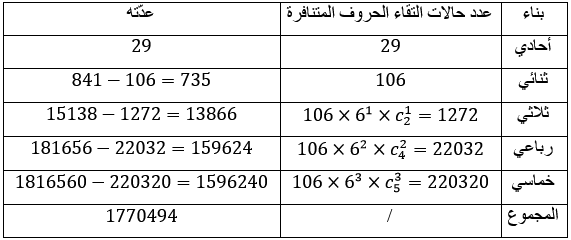
من خلال الجدول رقم (9) تبيّن أنّ هناك 106 ثنائية لا يقترن فيها حرفان، في الجدول رقم (11) التالي سنحسب عدد الأبنية المشكّلة من هذهِ الثنائيات ثمّ ننقصها من نتائج الجدول السابق فنتحصل على عدد الأبنية الممكن استعمالها في اللغة العربية بناء على القاعدتين 1 و 2:
خلاصة
من خلال اعتماد خاصيتين تتميّز بهما اللغة العربية وهما: لزوم وجود حروف الذلق والحروف الشفوية في الأبنية من جهة و من جهة أخرى استحالة اقتران حروف معيّنة بسبب تنافرها ـ تبيّن لنا أنّ عدد الأبنية الممكن استخدامها يفوق مليون وسبعمئة الف بناء وهو ما يمثّل نسبة 8.33 % من العدد النظري للأبنية في اللغة العربية؛ بينما عدد الأبنية المستعملة التي أوردها الزبيدي صاحب مختصر العين لا تمثّل سوى 0.31 % من العدد الذي أوجدناه؛ وأمام هذا الكمّ الهائل الذي لا أثر له في المعاجم الا ضمن المهمل يجدر بنا أن نطرح عدّة تساؤلات نرجئ اختبار مدى وجاهتها لما قد تفرزه أبحاث مستقبلية تميط اللثام عنها، ولعلّ أهمّ هذهِ التساؤلات:
هل تحمل هذهِ الأبنية المهملة المختفية معان لحالات مادّية أو معنوية تمّ الاستغناء عنها اقتصادا أو تعرّضت للإندثار؟ فمثلا في ترتيب سنّ البعير نجد الثعالبي في فقه اللغة يسرد له هذهِ الأسماء من الولادة الى الهرم:

ويمكن أن نطلق على هذه الظاهرة المميّزة للغة العربية "فصلنة المتصل" وهو ما يسمح بتوليد عدد معتبر من المعاني وبالتالي عدد معتبر من الأبنية.
- هل هناك قواعد أخرى لتنافر الحروف؟
- هل يمكن أن يمكن أن نجد معايير أخرى غير الاستثقال تكون أكثر معقولية للتمييز بين المستعمل والمهمل؟
شكر وتقدير: أتقدّم بجزيل الشكر الى الأستاذ عمر بن كَرُّوش لمراجعته هذهِ الورقة البحثية.
- ابن الأثير الكاتب، المثل السائر في أدب الكاتب والشاعر، تحقيق: أحمد الحوفي وبدوي طبانة، نهضة مصر، القاهرة، ج 3، ص 166.
- الخليل بن أحمد الفراهيدي، العين، تحقيق: د.مهدي المخزومي و د. إبراهيم السامرائي، الهلال، انظر المقدمة.
- خطأ وتصويبه: تسعة عشر؛ ولا نعلم مصدر الخطأ إن كان من المخطوط أو المطبوع.
- جلال الدين السيوطي، المزهر في علوم اللغة وأنواعها، المكتبة العصرية، بيروت، ج 1، ص: 74-75.
- المزهر، مرجع سابق، ص 59.
- علي حلمي موسى، دراسة تقنية مقارنة لمعاجم الصحاح ولسان العرب وتاج العروس، مجلة المعجمية، تونس، 1990، عدد 5-6، ص 149.
- ابن منعم العبدري، فقه الحساب، تقديم: ادريس لمرابط، دار الأمان، الرباط، ص 201.
- العين، مرجع سابق، انظر المقدمة.
- دراسة تقنية …، مرجع سابق، ص 109.
- أحمد بن محمد بن أحمد القرشي، الخلاف بين سيبويه والخليل في الصوت والبنية، مجلة جامعة أمّ القرى، ج 11، ص 385.
- محمد مراياتي، يحي ميرعلم، محمد حسن الطيان؛ علم التعمية واستخراج المعمّى عند العرب؛ مجمع اللغة العربية، دمشق، 1987، ج 1، ص 136، ص 191، ج 2، ص 142.
- Mahdi ABDELJAOUAD, Quelques éléments d'histoire de l'analyse combinatoire, Journées Nationales 2003 de l'ATSM, p3, p4.
- Ahmed DJEBBAR, L’analyse combinatoire au Maghreb: l’exemple D’Ibn Muncim (XIIe-XIIIe s), publications mathématiques d’Orsay, n0 85-01, p30, p86.
البريد الإلكتروني: ahmedrefice@gmail.com
الآراء الواردة في هذا المقال هي آراء المؤلفين وليست، بالضرورة، آراء منظمة المجتمع العلمي العربي.
يسعدنا أن تشاركونا أرائكم وتعليقاتكم حول هذهِ المقالة عبر التعليقات المباشرة بالأسفل أو عبر وسائل التواصل الإجتماعي الخاصة بالمنظمة





